 |
|
The basic logic functions and
equivalent gates |
|

|
Given a box with two
inputs A, B and one output Fx - How many logic functions
possible inside the box?
Answer:
Drag the mouse over the box below (hold the left button
down)
|
|
A |
B |
F0 |
F1 |
F2 |
F3 |
F4 |
F5 |
F6 |
F7 |
F8 |
F9 |
F10 |
F11 |
F12 |
F13 |
F14 |
F15 |
|
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
|
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
|
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
|
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
There's 16
possible functions but not all that useful and given a
name like: AND, NAND, OR, NOR, XOR, XNOR
|
| |
|
|
|
|
|
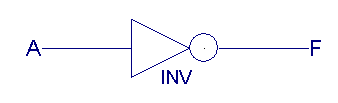
|
| A |
B |
F(AND) |
|
0 |
0 |
0 |
|
0 |
1 |
0 |
|
1 |
0 |
0 |
|
1 |
1 |
1 |
|
|
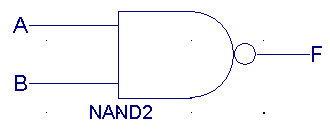
|
| A |
B |
F(NAND) |
|
0 |
0 |
1 |
|
0 |
1 |
1 |
|
1 |
0 |
1 |
|
1 |
1 |
0 |
|
|
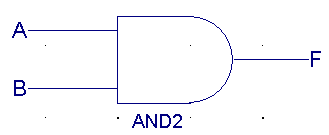
|
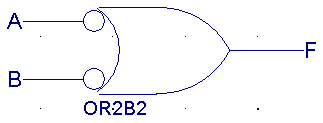
| A |
B |
F(OR) |
|
0 |
0 |
0 |
|
0 |
1 |
1 |
|
1 |
0 |
1 |
|
1 |
1 |
1 |
|
|

|
| A |
B |
F(NOR) |
|
0 |
0 |
1 |
|
0 |
1 |
0 |
|
1 |
0 |
0 |
|
1 |
1 |
0 |
|
|
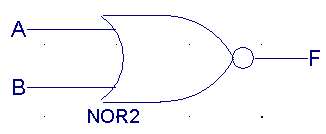
|
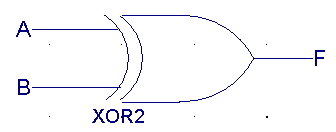
| A |
B |
F(XOR) |
|
0 |
0 |
0 |
|
0 |
1 |
1 |
|
1 |
0 |
1 |
|
1 |
1 |
0 |
|
|
|
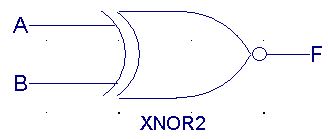
| A |
B |
F(XNOR) |
|
0 |
0 |
1 |
|
0 |
1 |
0 |
|
1 |
0 |
0 |
|
1 |
1 |
1 |
|
|
|
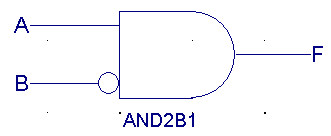
| A |
/B |
F(ANDb1) |
|
0 |
1 |
0 |
|
0 |
0 |
0 |
|
1 |
1 |
1 |
|
1 |
0 |
0 |
|
|
|
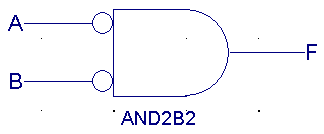
| /A |
/B |
F(NOR) |
|
1 |
1 |
1 |
|
1 |
0 |
0 |
|
0 |
1 |
0 |
|
0 |
0 |
0 |
|
 |
|
| A |
/B |
F(ORb1) |
|
0 |
1 |
1 |
|
0 |
0 |
0 |
|
1 |
1 |
1 |
|
1 |
0 |
1 |
|
|

|
| /A |
/B |
F(NAND) |
|
1 |
1 |
1 |
|
1 |
0 |
1 |
|
0 |
1 |
1 |
|
0 |
0 |
0 |
|
 |
|
| |
|
|
|
|
