#1

Boolesk Algebra og Digitalteknik

Last updated: 12-08-11

George Boole var i midten af 1800 tallet træt af at høre på folk som vrøvlede og besluttede sig for at opstille et sæt af regler som kunne bruges til at analyse udtryk bestående af udsagn som enten kunne være sande eller falske.

Ved at kombinere nedenstående regler kan man ofte reducere et udsagn (gøre det lettere at forstå) - og nok så vigtigt - man kan måske spare nogle logiske kredse = sparede penge og energi.

Specielt regel T10 er nyttig når man ønsker at reducere et logisk udtryk - Problemet er bare at få det store overblik som er nødvendigt.
Den franske ingeniør Karnaugh løste dette problem ved at udvikle en grafisk metode (Karnaugh kort) baseret på regel T10.
Desværre kan den kun bruges med fordel på logiske udsagn på optil 6 input.

Den Booleske algebra (inklusiv De Morgans regler)
.

Prøv at bevise / anskueliggøre De Morgans regler - Hint: lav sandhedstabeller

Eksempel:

Spørgsmål - Bør tolderne kontrollere det unge par?

Analoge og digitale signaler

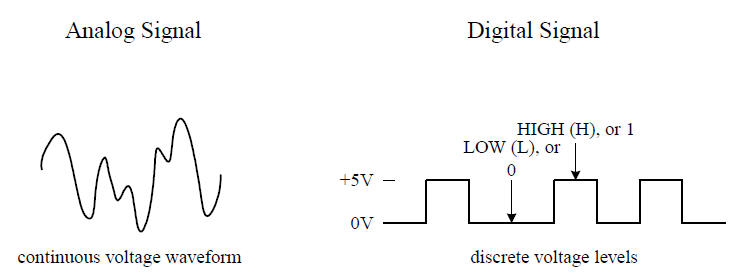
Verden er analog siges det .... Men man burde måske tilføje et endnu, for udviklingen de sidste 50 år har gået ud på, at gøre alt i vores i hverdag digitalt. Og der er vist ingen grund til at tvivle på at denne udvikling vil forsætte. Hvorfor digitalt er godt

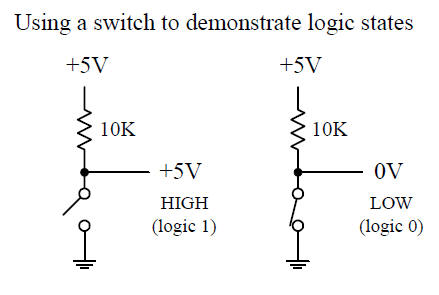
Digitale signaler er kendetegnet ved at de kan antage to værdier. En kontakt kan være ÅBEN og LUKKET. Hvis man kombinerer kontakten med en spændingskilde og en modstand vil kontakten kunne frembringe et digitalt elektrisk signal. TRUE = Logisk 1 = +5Volt FALSE = Logisk 0 = 0Volt	Hvorfor dog bruge en modstand? En moderne computer indeholder flere hundrede millioner logiske kredse og det er derfor vigtigt at disse kredse bruger så lidt strøm som muligt. Derfor bruger man CMOS kredse og spændings niveauet for logisk 1 prøver man at få langt ned som muligt (omkring 1,5 Volt)

Digitale kredse / funktioner - NOT AND OR - NAND NOR - XOR

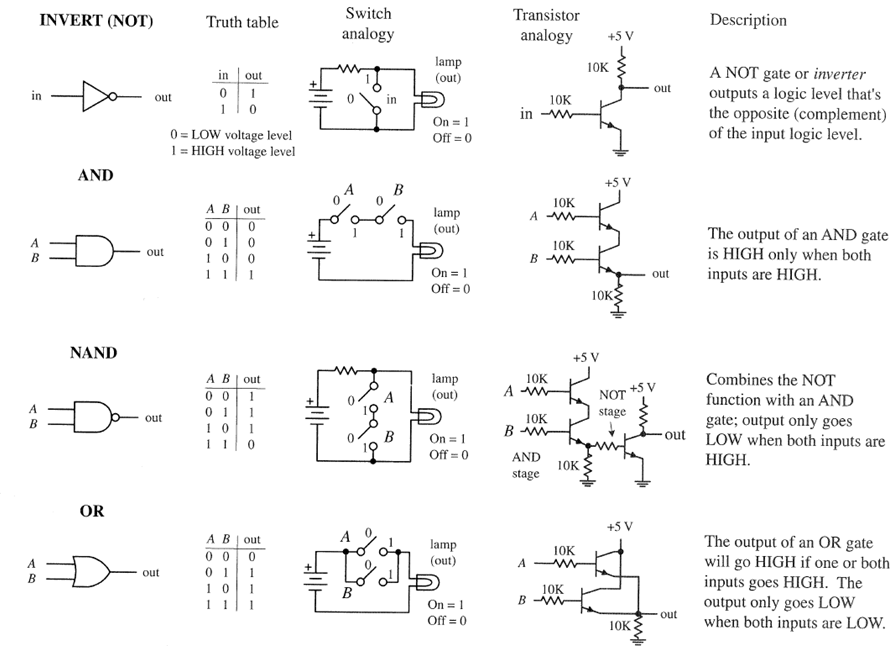
	Ved at kombinere NOT - AND - OR kredse kan man realisere ethvert logisk udtryk. Bemærk - en logisk kreds kan godt have mere end to indgange, måske lige bortset fra NOT kredsen. Påstand: Man behøver i virkeligheden kun at have skuffen fuld af NAND kredse - ethvert logisk udtryk kan laves udelukkende med disse.
Prøv her INV AND NAND OR

Man skelner imellem kombinatorisk og sekventiel logik.

Et kombinatorisk logikkredsløb består af et antal indgange og mindst en udgang. Når man giver indgangene en bestemt kombination af H og L vil man altid få den samme værdi på udgangen.

Hvis det drejer sig om et sekventielt kredsløb vil det (per definition) indeholde hukommelse og udgangsværdien kan således afhænge af både det aktuelle input og de værdier som har været på indgangene før.

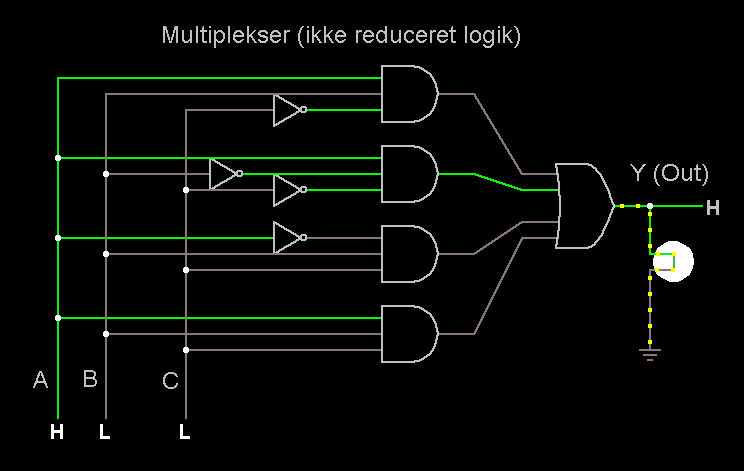
Mux - Eksempel på kombinatorisk logik (ikke reduceret logik)


C A B Y ------------------------------- L L L L L L H L L H L H L H H H H L L L H L H H H H L L H H H H
Sandhedstabel for multiplekser	Som det kan ses herover så vil ABC = HLL => Y = H Hvad sker der hvis ABC = HHL => Y = ? Prøv alle kombinationer af ABC og opstil en sandhedstabel .

En multiplekser kan med andre ord bruges til at vælge imellem 2 (eller flere) indgange ved hjælp af C (eller Select) indgangen.
Den valgte indgang vil således kunne aflæses på udgangen (Y)
.

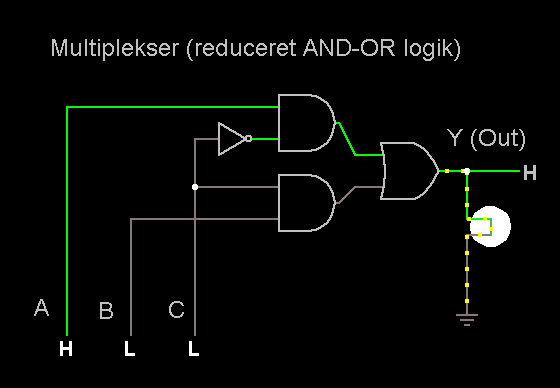
Mux - Eksempel på (reduceret) kombinatorisk logik
(AND-OR logik = Sum Of Products logik)
AND-OR logik kan altid omformes til NAND-NAND logik (og omvendt)

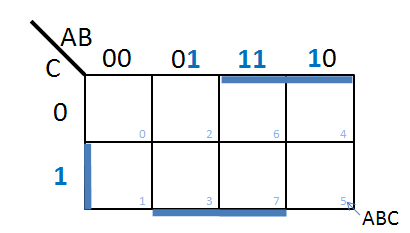
Prøv at reducere det logiske udtryk for multiplekseren

	Der er mange fordele (besparelser) ved et reduceret logisk udtryk
	.

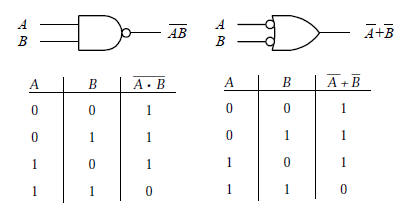
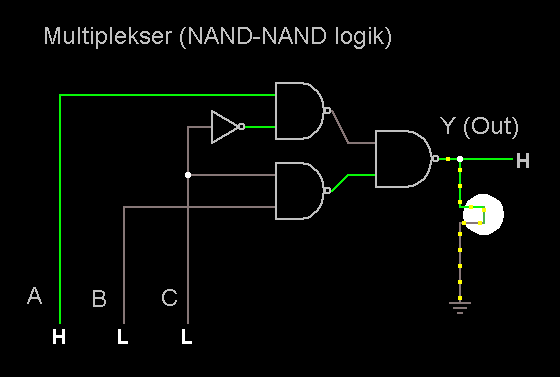
To forskellige måder at repræsentere en NAND kreds. (De morgans teori)	Man skal med andre ord kun have 2 input NAND kredse i skuffen, så kan alt lade sig gøre - Hvad med inverteren, kan den også erstattes af en 2 input NAND kreds?


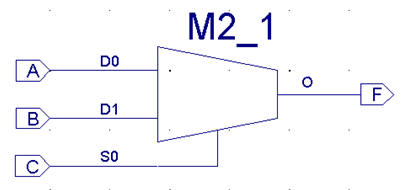
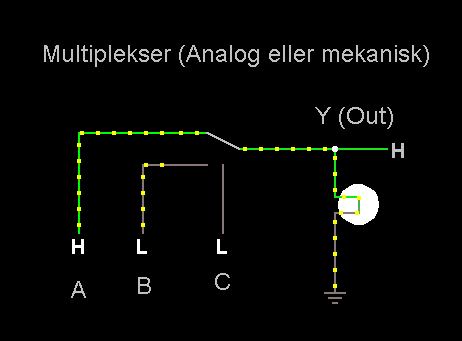
Normalt bekymrer man sig ikke om hvad der er "inde i" en multiplekser. Det er dens funktion der har betydning.	Multiplekser funktionen er meget vigtig og bruges i næsten alle former for apparater. (Gammeldags analoge og moderne digitale)

Der findes mange standard kredsløb inden for kategorien kombinatorisk logik. For eksempel findes der også det modsatte af multipleksere (Demultipleksere) ligesom Dekodere også er meget anvendte.
.

SR-Latchen - En hukommelse (1-bit) som kan Sættes og Nulstilles



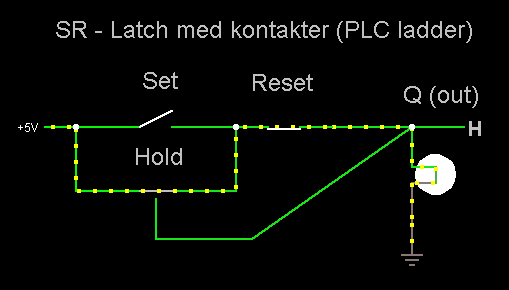
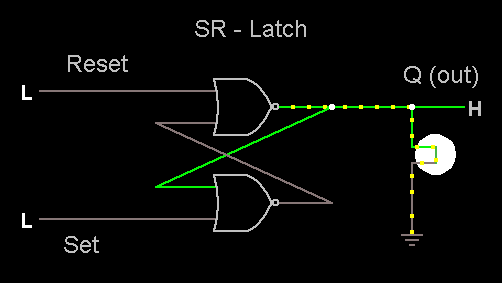
Ved hjælp at et Holdekredsløb kan man lave et hukommelses-bit ved hjælp af simple relækontakter.	Normalt er det IKKE tilladt at koble en udgang på et kombinatorisk kredsløb tilbage til en indgang. Men i dette tilfælde er resultatet meget nyttigt. (Prøv selv at lægge Reset og Set - H og L (alle 4 kombinationer)
Hvad har mest at skulle have sagt - Set eller Reset? .

Det er sjældent man har brug for en SR-Latch i forbindelse med digitale kredsløb. Men i forbindelse med PLC-programmering er denne funktionalitet meget brugt (Det er nærmest umuligt at lave et PLC - Ladder program uden at bruge S og R eller L og U).
.

D-Latchen - En hukommelse (1-bit) som kan åbnes og lukkes med C indgangen



	Bemærk hvordan D indgangen styrer udgangen Q når D-Latchen er åben (C=1) og hvordan Q huskes når C=0.

Denne type hukommelse er nogen gange brugt i forbindelse med digitale kredsløb og kan også finde anvendelse i forbindelse med PLC programmering. (Men man finder ikke normalt D-Latche i Ladder)	Man kan også vælge at lade D-Latchen åbne på et lavt niveau og lukke (huske) på et højt niveau.

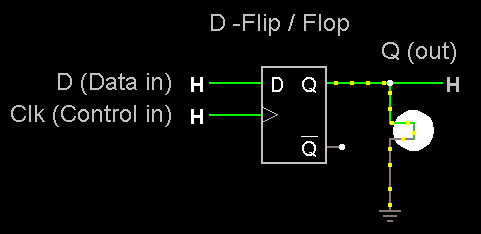
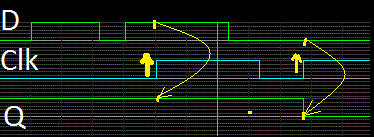
D-Flip/Flop - En hukommelse (1-bit) - aflæser D og husker på Q hver gang skifter fra 0 til 1

Hvis sætter man 2 D-Latche efter hinanden, kan man konstrueret en Kanttrigget D-Flip/Flop. Hvis den første D-latch åbner på Lavt niveau og den næste D-Latch åbner på Højt niveau får man en positiv Kanttrigget D-Flip/Flop



Alle former for digital elektronik (Computere, Mobiltelefoner, Fjernsyn etc.) er baseret på kombinatorisk logik i kombination med D-Flip/Flops Man finder ikke D-Flip/Flops i forbindelse med PLC-programmering (eller anden form for programmering) men man kan ofte have fordel af at detektere skift af signaler / variable. I forbindelse med Ladder programmering bruges ofte One-shots som netop detektere flanker.